칸아카데미의 알고리즘 코스를 들으며 정리해본 알고리즘 기초.
https://ko.khanacademy.org/computing/computer-science/algorithms

그래프 표현

• 그래프는 순환여부에 따라 순환, 비순환 그래프가 있다.
• 그래프는 방향여부에 따라 방향, 무방향 그래프가 있다.

[그래프에 대한 기본 용어]

• 정점(vertex): 그래프를 이루고 있는 어떠한 꼭짓점, 노드(node)
• 변(edge): vertex를 연결하는 선, 간선
• 차수(degree): edge의 수

[트리는 무엇인지?]

• 자료구조 중 트리(tree)는 그래프의 한 종류로써, 방향 비순환 그래프이다.
  • DOM 또한 대표적인 트리 구조이다.
  • 그래서 트리 중간에 엘리먼트를 추가하거나 삭제하면 해당 노드부터 트리를 다시 계산한다.
  • 또한 엘리먼트에 스타일을 부여해서 레이아웃이 바뀌어도 트리를 재계산한다.
  • 이때 해당 노드를 시작으로 모든 자식트리를 재계산해 재배치하는 것을 reflow라고 한다.
  • 이러한 특징 때문에 최대한 DOM의 말단 노드를 조작해야한다.

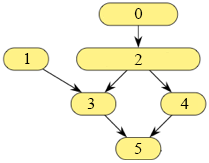
이러한 그래프가 있다고 하면, 변수에 저장할 때 3가지 방식으로 할 수 있겠다.

1. 엣지리스트 (Edge List)

엣지리스트는 두 vertex을 연결하는 edge의 개수만큼의 배열로 그래프를 저장하는 방식이다. 매우 간단한 방식이지만 아무런 순서 없이 무작위로 들어가 있다면, 특정 edge를 찾기 위해 선형 검색을 해야 하고 이는 O(N)만큼의 복잡도를 지닌다.

const edgeList = [
  [0, 2],
  [1, 3],
  [2, 3],
  [2, 4],
  [3, 5],
  [4, 5],
];

2. 인접행렬

인접행렬은 모든 vertex에 인접한 각 vertex를 0으로 표시하고 edge가 있는 경우 1로 표시한 배열로 그래프를 저장하는 방식이다. 즉, vertex by vertex로써 저장되므로 edge가 별로 없는 희소 그래프이더라도 공간을 N^2만큼 차지한다. 게다가 특정 i의 인접한 j를 찾기 위해서는 i행의 모든 vertex를 검색해야 한다.

const adjMatrix = [
  [0, 0, 1, 0, 0, 0],
  [0, 0, 0, 1, 0, 0],
  [0, 0, 0, 1, 1, 0],
  [0, 0, 0, 0, 0, 1],
  [0, 0, 0, 0, 0, 1],
  [0, 0, 0, 0, 0, 0],
];

3. 인접리스트

인접리스트는 각 vertex의 edge로 연결된 vertex로 이루어진 배열로 그래프를 저장하는 방식이다. 따라서 edge (i, j)가 그래프에 있는지 찾으려면 graph[i][j]로 검색해야 한다. 이 검색은 최악의 경우에는 정점 i의 edge 개수만큼 걸린다. 즉, O(degree)만큼의 복잡도를 지닌다.

const adjList = [[2], [3], [3, 4], [5], [5], []];

너비우선탐색, 거대한 그래프 횡단해보기

• 너비우선탐색은 주어진 소스 정점에서 다른 모든 정점에 이르기까지 거치는 edge의 수를 계산해 가장 짧은 경로를 찾는 알고리즘
• Breadth First Search, BFS라고도 불림
• 각 정점은 아래의 2가지 값을 지님
  • 거리: 어떠한 정점에서 특정 정점으로 이르는 아무 경로에 있는 edge의 최소 수
  • 선행 정점: 소스 정점에서 가장 짧은 경로 내 특정 정점의 선행자가 되는 정점이며, 소스 정점의 선행정점은 null과 같은 특수 값을 가지는데 이는 선행 정점이 없음을 의미

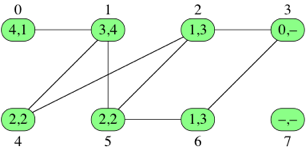
• 소스 정점 3부터 시작, 정점 3의 거리는 0
• 정점 2와 6에서 거리를 1로, 선행 정점을 정점 3으로 설정 (소스에서 거리가 0)
• 정점 4와 5에서 거리를 2로, 선행 정점을 정점 2로 설정 (소스에서 거리가 1)
• 정점 1로 가서 거리를 3으로, 선행 정점을 정점 4로 설정 (소스에서 거리가 2)
• 정점 0으로 가서 거리를 4로, 선행 정점을 정점 1로 설정 (소스에서 거리가 3)
• 소스에서 거리가 4인 정점은 정점 0과 1뿐인데 이미 방문했으니 끝!

Q1. 어떤 정점에 이미 갔는지 여부를 어떻게 결정하는가?
방문하기 전에는 정점의 거리가 null일 것이고 가보게 되면 거리에 따라 값이 할당된다. 따라서 어떤 정점의 이웃 정점을 검사할 때 그 거리가 현재 null인 정점만 방문하면 된다.

Q2. 어떤 정점에 이미 갔으나, 거기서 출발했는지 여부를 어떻게 확인하는가?

• 선입선출(first in, first out)로 작동하는 큐(queue)를 사용하면 된다.
  • enqueue(obj)는 큐에 객체를 삽입
  • dequeue()는 가장 오래 큐에 있었던 객체를 큐에서 제거하고 이 객체를 반환
  • isEmpty()는 현재 큐에 객체가 없으면 true, 큐에 하나 이상의 객체가 있으면 false 반환