Algorithm basic 2

2020-05-13

computer-science

칸아카데미의 알고리즘 코스를 들으며 정리해본 알고리즘 기초.
https://ko.khanacademy.org/computing/computer-science/algorithms

좀더 빠른 정렬? feat. 재귀적 알고리즘 설계

선택정렬과 삽입정렬의 최대 실행시간은 O(n^2)이다. 따라서 입력하는 배열의 크기가 크다면 매우 오랜 시간이 걸린다. 하지만 재귀를 활용하면 더 빠르게 정렬할 수 있다. 각 정렬의 실행시간은 다음과 같다.

sort

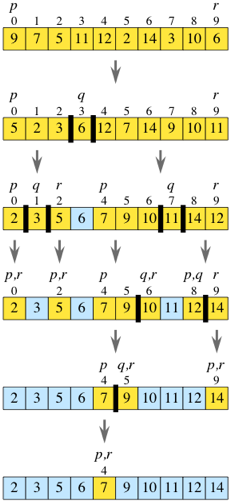
[병합정렬 (merge sort)]

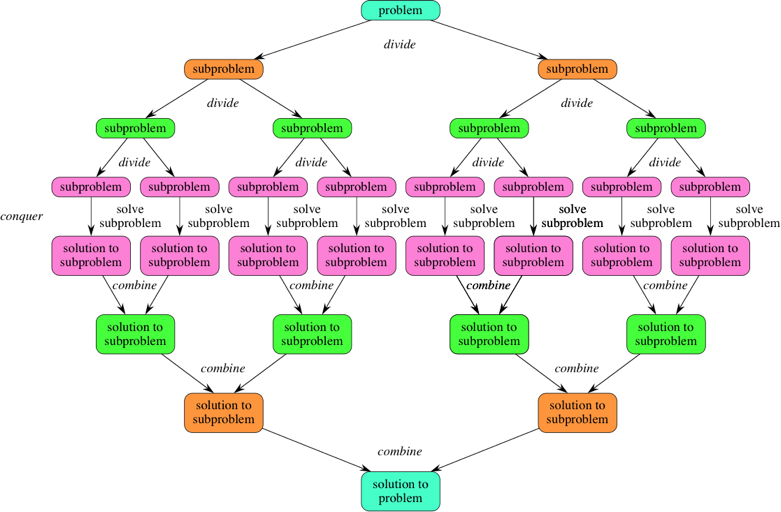
merge-sort

분할 정복 (divide and conquer)식 알고리즘 ?

재귀 알고리즘 설계 패러다임을 기반으로 삼고 있다.
한 문제를 비슷한 여러 개의 하위 문제로 나누어 재귀적으로 해결하고 이를 합쳐 원래 문제를 해결한다.
단계
1. 분할: 원래 문제를 분할하여 비슷한 유형의 더 작은 하위 문제들로 나눈다.
2. 정복: 하위 문제 각각을 재귀적으로 해결한다. 하위 문제의 규모가 충분히 작으면 문제를 탈출 조건으로 지정한다.
3. 병합: 하위 문제들의 배열을 합쳐서 원래 문제를 해결한다.

예시: javascript

const merge = function (array, p, q, r) {
  let leftHalf = [];
  let rightHalf = [];
  let k = p;
  let i = 0;
  let j = 0;

  for (i; k <= q; i++, k++) leftHalf[i] = array[k];
  for (j; k <= r; j++, k++) rightHalf[j] = array[k];

  k = p;
  i = 0;
  j = 0;

  while (i < leftHalf.length && j < rightHalf.length) {
    if (leftHalf[i] < rightHalf[j]) {
      array[k] = leftHalf[i];
      i++;
    } else {
      array[k] = rightHalf[j];
      j++;
    }

    k++;
  }

  while (i < leftHalf.length) {
    array[k] = leftHalf[i];
    k++;
    i++;
  }

  while (j < rightHalf.length) {
    array[k] = rightHalf[j];
    k++;
    j++;
  }
};

function mergeSort(array, p, r) {
  if (p < r) {
    const q = Math.floor((p + r) / 2);

    mergeSort(array, p, q);
    mergeSort(array, q + 1, r);
    merge(array, p, q, r);

    return array;
  }
}

정렬하는 배열의 인덱스 범위는 p..r이며, 중간 인덱스 q를 지정하여 분할-정복한다.
q를 기준으로 왼쪽과 오른쪽을 돌며 최소값을 찾아 초기값이 p인 k위치에 복사한다.
결국 하위배열의 최소값이 차곡차곡 배열의 k위치에 복사된다.
왼쪽이나 오른쪽 하위배열에 남은 값이 있다면 그대로 복사하면 된다.

—> 병합과정에서 두 요소만을 비교하고 각 요소는 최대 한 번의 비교로 array로 다시 복사된다. 따라서 병합하는 과정은 입력값 n만큼의 복잡도를 지닌다. 그리고 분할-정복을 재귀적으로 반복할 때에는 처리할 입력값 n이 n/2, n/4, n/8... 의 형태로 줄어든다. 따라서 병합정렬의 실행시간은 O(n logn)이다.

—> 병합정렬은 계속 왼쪽과 오른쪽의 하위배열 복사본을 만들어야 하여 저장공간이 필요하다. 즉, 이 정렬은 정렬할 배열이 저장된 그 자리에서 작동하지 않는다.

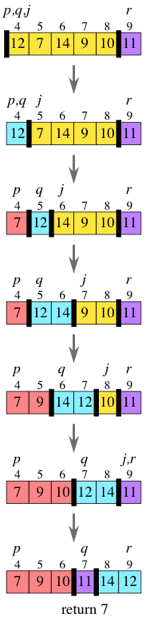
[퀵정렬 (quick sort)]

quick-sort

병합정렬처럼 분할 정복식 전략을 사용하는 재귀 알고리즘이다.
병합단계에서 주요 작업이 이루어지는 병합정렬과 달리, 분할 단계에서 주요 작업이 이뤄진다.
제자리에서 작동하지 않는 병합정렬과 달리, 제자리에서 작동한다.
최악의 경우는 n^2이지만, 매 단계에서 적어도 1개 원소가 자리를 찾게 되므로 일반적으로 다른 알고리즘에 비해 실제로는 성능이 좋다.

예시: javascript

const swap = function (array, firstIndex, secondIndex) {
  const temp = array[firstIndex];

  array[firstIndex] = array[secondIndex];
  array[secondIndex] = temp;
};

const partition = function (array, p, r) {
  let q = p;

  for (let i = p; i < r; i++) {
    if (array[i] <= array[r]) {
      swap(array, i, q);
      q++;
    }
  }

  swap(array, r, q);

  return q;
};

const quickSort = function (array, p, r) {
  if (p < r) {
    const q = partition(array, p, r);

    quickSort(array, p, q - 1);
    quickSort(array, q + 1, r);
  }
};

하위배열에서 아무 요소를 기준점으로 고른다. 이를 피벗(pivot)이라고 한다. 여기서는 하위배열의 가장 오른쪽 요소인 array[r]을 피벗으로 선택하고 이 피벗이 나중에 올 자리가 q가 된다. 즉, p..r범위를 돌며 값을 swap하다가 맨 오른쪽이었던 r위치에 있는 값이 자리를 찾으면 그 인덱스가 q가 되며 파티션 과정이 종료된다.
피벗보다 작거나 같으면 왼쪽, 나머지는 모두 오른쪽으로 보낸다. 이 과정을 파티션(partition)이라고 한다.
피벗의 왼쪽과 오른쪽을 재귀적으로 정렬한 후 그대로 결합한다.

—> 하위 배열의 파티션을 나누는 데는 n만큼의 시간이 걸린다.

파티션하는 과정 ?

partition