Algorithm basic 1

2020-05-11

computer-science

칸아카데미의 알고리즘 코스를 들으며 정리해본 알고리즘 기초.
https://ko.khanacademy.org/computing/computer-science/algorithms

알고리즘

어떤 문제를 해결하기 위한 절차의 집합
컴퓨터 과학에서 알고리즘은 프로그램이 어떤 문제를 해결하기 위해 필요한 명령어들의 집합

시간 복잡도 Big-O

big-o

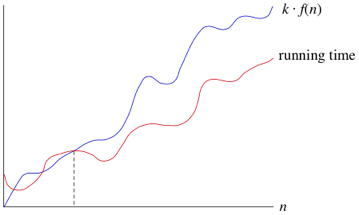
실행 시간의 효율성을 논의할 때 최악의 경우를 따져보는 것이 가장 일반적이다. 가장 대표적인 Big-O 계산법 또한 실행 시간의 최악의 경우를 따져보는 것으로, “실행 시간은 최대한 이만큼 커지지만 더 천천히 커질 수도 있다"라는 의미의 점근적 표기법이다.

[참고]

Big-θ는 최악과 최선의 경우 모두 고려하는 방식
Big-Ω는 최선의 경우만 고려하여 “실행시간은 최소한 이만큼 걸린다"라는 의미이다.

complexity

1. 지수함수(x^n) -> 거듭제곱 수가 상수가 아니면 더 가파르게 복잡도 증가
2. (거듭제곱 수가 상수인) 다항함수(n^x)
3. 선형함수(n)
4. 로그함수
5. 상수

일반적으로 x가 상수이고 n이 1부터 시작한다고 하면, 아래의 순서대로 실행시간이 천천히 늘어난다. 즉, 1번이 가장 복잡도가 큰 경우이다.

알고리즘의 실행 시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존
이 속도는 컴퓨터의 처리속도, 사용된 언어 종류, 프로그래밍 언어를 컴퓨터가 실행할 수 있는 코드로 바꾸는 컴파일러의 속도 등에 달려있다.
그러나 복잡도를 계산한다는 것은 입력값의 크기에 따라 이 함수가 얼마나 빨리 커지는지 알아보는 것에 가깝다.
따라서 프로그램을 쉽게 유지할 수 있도록 불필요한 부분은 버리고 가장 중요한 부분만 추려내서 함수를 간소화한다.

ex) 입력값 n에 따라 어떠한 알고리즘이 6n^2 + 100n + 300
만큼의 복잡도를 가진다면?

-> n이 대충 30 정도만 되어도 6n^2이 나머지 식들보다 커짐.
-> 즉, n^2에 의해 기하급수적으로 실행시간이 늘어남
-> 앞에 계수 6은 큰 영향을 주지 못하므로 해당 알고리즘의 복잡도는 n^2

로그함수? feat. O(log n)이 지니는 의미

로그(logarithm)는 “특정 밑(base)에 대한 거듭제곱 수"를 의미한다. 예를 들면, 밑이 2이고 진수가 8인 로그의 값은 3이다.

보통 프로그래밍에서는 밑을 2로 한다. 아마도 컴퓨터가 2진수이기 때문이라고 추측.
따라서 로그함수는 입력값 n이 늘어날 수록 필요한 값들의 범위를 반으로 줄인다.

예시: 이진검색 (javascript)

function binarySearch(array, target) {
  let guess = 0;
  let min = 0;
  let max = array.length - 1;

  while (max >= min) {
    guess = Math.floor((max + min) / 2);

    if (array[guess] === target) {
      return guess;
    } else if (array[guess] < target) {
      min = guess + 1;
    } else {
      max = guess - 1;
    }
  }

  return -1;
}

배열에 값이 16개 있을 경우?

첫 번째 탐색에서 최소 8개의 값을 제외시켜 남는 8개의 값에 대해 탐색 시작
두 번째 탐색에서 최소 4개의 값을 제외시켜 남는 4개의 값에 대해 탐색 시작
세 번째 탐색에서 최소 2개의 값을 제외시켜 남는 2개의 값에 대해 탐색 시작
네 번째 탐색에서 최소 1개의 값을 제외시켜 남는 1개의 값에 대해 탐색 시작
다섯 번째 탐색에서 1개의 값만 남아있으므로 리턴

—> 따라서 최대 5번만 탐색하면 된다.
—> O(log n) 복잡도는 이처럼 찾는 범위를 계속 줄여주므로 효율적이라고 할 수 있다.
—> 쉽게 말하면 반으로 쪼개서 필요없는 범위는 찾지 않도록 한다는 것이며, 실무에서도 필요없는 값을 반복하는 경우가 있는데 이때 로거리즘 기법을 생각해볼 수 있겠음!

재귀는 무엇인가 ?

recursion

재귀는 자기 자신을 호출하는 방식이다?

-> 이 설명은 재귀를 ‘어떻게’ 사용하는 지를 알려주는 것에 가깝다.
-> 즉, 재귀가 무엇인지는 100% 담을 수 없는 설명인 것 같다.

[재귀란]

어떤 문제를 해결하기 위해 알고리즘을 설계할 때 동일한 문제의 조금 더 작은 경우를 해결함으로써 그 문제를 해결하는 것.
문제가 간단해져서 바로 풀 수 있는 문제로 작아질 때까지 반복하는 것이며, 이런 테크닉을 재귀라고 함.
따라서 바로 풀 수 있는 문제가 되는 조건이 필요하며, 이를 탈출 조건(base case) 이라고 부름.

[재귀의 반복 조건]

재귀의 호출은 같은 문제 내에서 더 범위가 작은 값, 즉, 하위 문제에 대해 이루어져야 한다.
재귀함수 호출은 더 이상 반복되지 않는 base case에 도달해야 한다.

예시: 팩토리얼 (javascript)

const factorial = function (n) {
  if (n === 0) {
    return 1;
  }

  return n * factorial(n - 1);
};

n이 3인 경우 ?

3은 base case인 0이 아니므로 3 * factorial(3 - 1)
2는 0이 아니므로 3 _ 2 _ factorial(2 - 1)
1은 0이 아니므로 3 _ 2 _ 1 * factorial(1 - 1)
0은 0이므로 1을 반환하고, 결과값은 3 _ 2 _ 1 * 1

—> 이렇게 탈출 조건을 지정하면서 동일한 작은 태스크를 반복할 수 있는 형태라면 재귀 알고리즘을 사용할 수 있다.
—> 입력값이 n개라면 n만큼 자기 자신을 호출하기 때문에 시간복잡도 O(n)

최근에 알게 된 알고리즘 기법 ?

Brute force (무차별 대입 공격)

가능한 모든 경우의 수를 반복, 조작하며 결과값을 얻는 기법
Greedy (탐욕 알고리즘)

여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식

Sliding window

- 윈도우의 사이즈가 3일 때 아래 배열 탐색

[a b c d e f g h]

[a b c]
  [b c d]
    [c d e]
      [d e f]
        [e f g]
          [f g h]

Two pointer: 요소를 가르킬 포인터 2개를 조작하며 결과값을 얻는 기법, 아래 문제 (javascript)처럼 처음과 끝을 가리키며 점차 범위를 좁혀갈 때 많이 활용할 수 있다!

—> 입력값 n개에 대해 최악의 경우 n번을 반복해야 하므로 시간복잡도 O(n)

/**
 * Container With Most Water
 * - 주어지는 물의 높이값 배열에서 가장 물을 많이 담을 수 있는 구역 찾기
 * ex) [1,8,6,2,5,4,8,3,7] -> 49
 * 계산해보면 1번째 인덱스(a)부터 8번째 인덱스(b)까지의 차이 * MIN(height[a], height[b])
 */
const maxArea = function (height) {
  let area = 0;
  let left = 0;
  let right = height.length - 1;

  while (left < right) {
    area = Math.max(
      area,
      Math.min(height[left], height[right]) * (right - left)
    );

    if (height[left] < height[right]) left++;
    else right--;
  }

  return area;
};

Eratosthenes sieve (에라토스테네스의 체): N까지의 소수를 구할 때 최적의 방법. N까지 담겨있는 일종의 체에서 2의 배수, 3의 배수… i의 배수를 걸러내면서 루프를 돌면 마지막에는 소수만 남게 된다.

/*
 * 소수 (prime number)
 * - 원래 n까지 돌면서 n보다 작은 수까지만 n과 나누어 나머지가 0이 아닌 수를 소수로 체크했으나, 효율성이 낮음
 * - n까지의 소수 구하기에 최적화된 방법은 에라토스테네스의 체 알고리즘임
 * - n까지의 수를 담은 배열이 있고, 그 배열에서 2의 배수, 3의 배수, ... i의 배수를 계속 지우면 소수만 남게 됨
 */
function solution(n) {
  const dp = Array(n + 1);

  // O(n)
  for (let i = 2; i <= n; i++) dp[i] = i;

  // O(log n)
  for (let i = 2; i <= n; i++) {
    if (dp[i] === 0) continue;

    // i를 포함한 i의 배수를 구해 지움
    for (let k = i * 2; k <= n; k += i) {
      dp[k] = 0;
    }
  }

  return dp.filter((v) => v > 0).length;
}